Intervalo (matemática)
De Wikipedia, la enciclopedia libre
En matemáticas, un intervalo (del lat intervallum) es un conjunto comprendido entre dos valores. Específicamente, un intervalo real es un subconjunto conexo de la recta real, es decir, una porción de recta entre dos valores dados.
 es la parte de
es la parte de  que verifica la siguiente propiedad:
que verifica la siguiente propiedad:




La siguiente tabla resume los 11 casos posibles, con a ≤ b, y x perteneciente al intervalo:
Entonces: a + c ≤ x + y ≤ b + d. Lo que justifica que
 , los intervalos son las bolas abiertas y cerradas.
, los intervalos son las bolas abiertas y cerradas.
Un intervalo n-dimensional se define como un subconjunto de , que es el producto cartesiano de n intervalos:
, que es el producto cartesiano de n intervalos:  , uno en cada eje de coordenadas.
, uno en cada eje de coordenadas.
De manera más general, se le llama vecindad o entorno de centro a y radio ε, al conjunto de puntos x cuya distancia a a es menor que ε.
Contenido[ocultar] |
[editar] Caracterización
El intervalo real es la parte de
es la parte de  que verifica la siguiente propiedad:
que verifica la siguiente propiedad:Si |
[editar] Notación
Existen dos notaciones principales: en un caso se utilizan corchetes y corchetes invertidos, en el otro corchetes y paréntesis; ambas notaciones están descritas en el estándar internacional ISO 31-11.[editar] Intervalo abierto
No incluye los extremos. o bien
o bien ![]a,b[\](http://upload.wikimedia.org/wikipedia/es/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)
- Notación conjuntista o en términos de desigualdades:

[editar] Intervalo cerrado
Sí incluye los extremos.![[a,b]\](http://upload.wikimedia.org/wikipedia/es/math/c/f/c/cfcbcc2c2a41716ab844e25069e87453.png)
- Notación conjuntista o en términos de desigualdades:

[editar] Intervalo semiabierto
Incluye únicamente uno de los extremos. o bien
o bien  , notación conjuntista:
, notación conjuntista: 
![(a,b]\](http://upload.wikimedia.org/wikipedia/es/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](http://upload.wikimedia.org/wikipedia/es/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) , notación conjuntista:
, notación conjuntista: 
- Si a > b, los intervalos descritos no poseen elementos y denotan al conjunto vacío.
- (a,a), [a,a) y (a,a] denotan también al conjunto vacío.
- [a,a] denota al conjunto unitario {a}, también llamado intervalo degenerado.
- Estas notaciones también se utilizan en otras áreas de las matemáticas; por ejemplo, la notación
 , denota un par ordenado en teoría de conjuntos; las coordenadas de un punto o un vector en geometría analítica y álgebra lineal; un número complejo en álgebra.
, denota un par ordenado en teoría de conjuntos; las coordenadas de un punto o un vector en geometría analítica y álgebra lineal; un número complejo en álgebra. - Ambas notaciones admiten el símbolo
 para indicar que no hay cota.
para indicar que no hay cota.
[editar] Ejemplos



[editar] Clasificación
Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados, semiabiertos) o según sus características métricas (longitud: nula, finita no nula, infinita).La siguiente tabla resume los 11 casos posibles, con a ≤ b, y x perteneciente al intervalo:
| Notación | Intervalo | Longitud | Descripción |
|---|---|---|---|
![[a, b] \,](http://upload.wikimedia.org/wikipedia/es/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) | 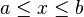 |  | Intervalo cerrado de longitud finita. |
 | 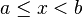 |  | Intervalo semiabierto (cerrado en a, abierto en b). |
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](http://upload.wikimedia.org/wikipedia/es/math/e/4/b/e4b1a75b94248c132a2083631c5283ed.png) |  |  | Intervalo semiabierto (abierto en a, cerrado en b). |
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](http://upload.wikimedia.org/wikipedia/es/math/8/8/9/88947e067526d5a6c30647a6101512f0.png) | 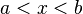 |  | Intervalo abierto. |
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](http://upload.wikimedia.org/wikipedia/es/math/f/6/f/f6f5ddc27f219da80f9e5f3cbd4c4ae8.png) |  |  | Intervalo semiabierto. |
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](http://upload.wikimedia.org/wikipedia/es/math/8/f/8/8f8009f0d0f4cd6d1001ef19fef4fbc8.png) |  |  | Intervalo semiabierto. |
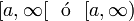 |  |  | Intervalo semiabierto. |
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](http://upload.wikimedia.org/wikipedia/es/math/8/e/6/8e62b6ce3cbde6646d2cd2dda6a5b6bc.png) |  |  | Intervalo semiabierto. |
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](http://upload.wikimedia.org/wikipedia/es/math/2/7/2/2724be6b6669686b27283fab7c37610d.png) |  |  | Intervalo a la vez abierto y cerrado. |
 |  |  | Intervalo cerrado de longitud nula (intervalo degenerado). |
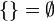 | x no existe | Sin longitud. | Conjunto vacío. |
[editar] Propiedades
- La intersección de intervalos de
 es también un intervalo.
es también un intervalo. - La unión de intervalos de
 no siempre es un intervalo (lo será si la intersección es no vacía).
no siempre es un intervalo (lo será si la intersección es no vacía). - Las partes conexas de
 son exactamente los intervalos.
son exactamente los intervalos. - Los intervalos cerrados son lo que se denominada «segmento de recta».
- La imagen por una función continua de un intervalo de
 es un intervalo de
es un intervalo de  . Esta es una formulación del Teorema del valor intermedio.
. Esta es una formulación del Teorema del valor intermedio.
[editar] Aritmética de intervalos
Sean I = [a, b] y J = [c, d] con a ≤ x ≤ b, y c ≤ y ≤ d.Entonces: a + c ≤ x + y ≤ b + d. Lo que justifica que
- I + J = [ a + c , b + d ].
- I - J = [ a - d, b - c ].
- Si se toman a, b, c y d positivos no nulos, I · J = [ ac, bd ] y I / J = [ a/d, b/c ].
[editar] Generalización
En el espacio métrico , los intervalos son las bolas abiertas y cerradas.
, los intervalos son las bolas abiertas y cerradas.Un intervalo n-dimensional se define como un subconjunto de
 , que es el producto cartesiano de n intervalos:
, que es el producto cartesiano de n intervalos:  , uno en cada eje de coordenadas.
, uno en cada eje de coordenadas.De manera más general, se le llama vecindad o entorno de centro a y radio ε, al conjunto de puntos x cuya distancia a a es menor que ε.
 e
e  pertenecen a
pertenecen a  , entonces para todo
, entonces para todo  tal que
tal que 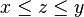 , se tiene que
, se tiene que 
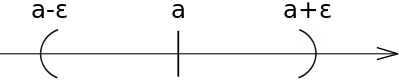
No hay comentarios:
Publicar un comentario